Zadania úloh
PRÍKLADY NA ZHODNÉ ZOBRAZENIE
- Daná je kružnica k(S;r) a jej vonkajší bod A. Zostrojte dotyčnice kružnice k s jej dotyčnicou prechádzajúcou bodom A bez použitia Talesovej kružnice. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daná jeho ťažnica ta a jeho výšky vb, vc. RIEŠENIE
- Zostrojte trojuholník ABC, ak poznáte a+b, va, c. RIEŠENIE
- Zostrojte trojuholník ABC, ak poznáte a, b,
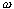 =
=  -
-  (
( je uhol BAC,
je uhol BAC,  je uhol ABC,
je uhol ABC,  >
>  , a > b). RIEŠENIE
, a > b). RIEŠENIE
- Daná je priamka MN a dve rôzne kružnice k1, k2 ležiace v tej istej polrovine vzhľadom na priamku MN, ktoré s ňou nemajú spoločný bod. Na priamke MN zostrojte taký bod X, aby dotyčnice vedené z bodu X ku kružniciam k1, k2 zvierali s priamkou MN zhodné uhly. RIEŠENIE
- Zostrojte spoločné dotyčnice dvoch kružníc k1(S1; r1), k2(S2; r2), ktoré nemajú spoločný bod a jedna neleží vo vnútri druhej, pričom r1
 r2 bez použitia rovnoľahlosti. RIEŠENIE
r2 bez použitia rovnoľahlosti. RIEŠENIE
- Zostrojte rovnoramenný trojuholník ABC, ktorého vrcholy ležia na troch sústredných kružniciach k1(S; r1), k2(S; r2), k3(S; r3). RIEŠENIE
PRÍKLADY NA ROVNOĽAHLOSŤ
- K danému trojuholníku ABC zostrojte rovnoľahlé trojuholníky A1B1C1, A2B2C2 v rovnoľahlosti H danej stredom S ležiaceho mimo trojuholníka ABC a koeficientom:
- h1=3/5,
- h2= -3/5. RIEŠENIE
- Určte šírku rieky, ktorej druhý breh je neprístupný. RIEŠENIE
- Narysujte všetky spoločné dotyčnice k dvom rôznym kružniciam, ktoré nemajú spoločný žiaden bod a jedna neleží vo vnútri druhej. RIEŠENIE
- Do daného konvexného kruhového výseku KSL vpíšte štvorec ABCD tak, aby trojuholník ABC bol rovnoramenný so základňou AB. RIEŠENIE
- Zostrojte kružnicu dotýkajúcu sa danej kružnice m(O; r) a danej priamky p v bode T (Pappova úloha). RIEŠENIE
- Dané sú dve rôznobežky a, b a kružnica k(K; r), ktorá sa nedotýka žiadnej z nich. Zostrojte kružnicu l, ktorá sa dotýka súčastne a, b, k. RIEŠENIE
PRÍKLADY NA PODOBNOSŤ
- Dokážte, že S1, S2, S3, S4 strán AB, BC, CD, AD ľubovoľného štvoruholníka ABCD sú vrcholmi rovnobežníka. Zistite kedy tento rovnobežník bude obdĺžnik, štvorec, kosodĺžnik, kosoštvorec? RIEŠENIE
- Dokážte, že dĺžky výšok va, vb, vc trojuholníka ABC sú nepriamo úmerné dĺžkam strán a, b, c. RIEŠENIE
- Základne lichobežníka ABCD majú dĺžky a, b. Nájdete dĺžku úsečky YZ vyťatej uhlopriečkami AC, BD na strednej priečke XQ lichobežníka ABCD. RIEŠENIE
- Deltoid ABCD má os súmernosti AC a jeho uhly pri vrcholoch B, D sú pravé. Vyjadrite polomer kružnice vpísanej do deltoidu pomocou dĺžok jeho strán. RIEŠENIE
- Zostrojte rovnoramenný trojuholník ABC, ak je daný uhol
 pri jeho základni a súčet výšok vc + va. RIEŠENIE
pri jeho základni a súčet výšok vc + va. RIEŠENIE
- Je daný vypuklý štvoruholník ABCD s plochov S a bod M, ktorý leží v štvoruholníku. Symetrickými obrazmi stredov strán štvuruholníka ABCD podľa stredu M sú body P, Q, R, T. Určte plochu štvoruholníka PQRT. RIEŠENIE
PRÍKLADY NA KONŠTRUKCIU TROJUHOLNÍKOV
- Zostrojte trojuholník ABC, ak poznáte
 ,
,  a výšku vc. RIEŠENIE
a výšku vc. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daná strana a, výšky vb, vc (vb, vc ležia v tej istej polrovine vzhľadom na priamku BC, vb
 a
a vc). RIEŠENIE
vc). RIEŠENIE
- Zostrojte trojuholník ABC, ak je daný bod M, ktorý je pätou kolmice z vrcholu A na stranu BC; bod N, ktorý je pätou kolmice z vrcholu B na stranu AC a priamka p, na ktorej leží strana AB. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daný polomer r opísanej kružnice, výška vc a ťažnica tc. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daný jeho obvod a + b + c a uhly
 a
a 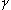 . RIEŠENIE
. RIEŠENIE
- Zostrojte rovnoramenný trojuholník ABC vpísaný do danej kružnice k(S; r), ak je daný súčet a + v veľkosti jeho základne a príslušnej výšky. RIEŠENIE
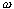 =
=  -
-  (
( je uhol BAC,
je uhol BAC,  je uhol ABC,
je uhol ABC,  >
>  , a > b). RIEŠENIE
, a > b). RIEŠENIE
 r2 bez použitia rovnoľahlosti. RIEŠENIE
r2 bez použitia rovnoľahlosti. RIEŠENIE
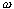 =
=  -
-  (
( je uhol BAC,
je uhol BAC,  je uhol ABC,
je uhol ABC,  >
>  , a > b). RIEŠENIE
, a > b). RIEŠENIE
 r2 bez použitia rovnoľahlosti. RIEŠENIE
r2 bez použitia rovnoľahlosti. RIEŠENIE
 pri jeho základni a súčet výšok vc + va. RIEŠENIE
pri jeho základni a súčet výšok vc + va. RIEŠENIE
 ,
,  a výšku vc. RIEŠENIE
a výšku vc. RIEŠENIE
 a
a vc). RIEŠENIE
vc). RIEŠENIE
 a
a 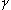 . RIEŠENIE
. RIEŠENIE