Prvý trojuholník A1B1C1 (pre h=3/5) dostaneme tak, že úsečku SA rozdelíme na 5 rovnakých dielov. Bod A1 potom umiestnime do bodu, ktorý delí úsečku SA v pomere 3:2 (|SA1|:|A1A|=3:2). Bude teda platiť:
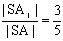
Vrcholy B1, C1 ležia na polpriamke SB, SC a to tak, že AB || A1B1, AC || A1C1 (postup vyplýva z vlastnosti rovnoľahlosti, že obraz úsečky je v rovnoľahlosti úsečka s ňou rovnobežná).