Zostrojte 4-uholník ABCD s rozmermi AB, BC, AC, BD a uhlom d = |CDA|.


Na riešenie tejto úlohy sme využili množinu "G" a vlastnosti uhlopriečok. 

Narysujte úsečku AB. Potom zostrojte bod C. C je je prienikom kružníc m a n, kde m je množinou všetkých bodov, ktoré sú vzdialené od B |BC| a n je množinou bodov, ktoré sú vzdialené od A |AC|. Bod D patrí množine G "nad" AC a kružnici k, ktorá je zostrojená z B s polomerom |BD|.



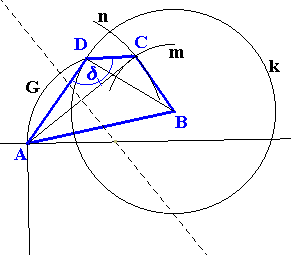
Náčrt

Rozbor:

Postup konštrukcie:
d = ADC

vrchol C:
     * C m; m (B, |BC| )
     * C n; n (A, |AC| )
     * C m n

vrchol D:
     * D G
     * D k; k (B, |BD| )
     * D G k
   1. AB
  2. m; m (B, |BC| )
  3. n; n (A, |AC| )
  4. m n = {C}
  5. G = { D E2; | ADC| = d }
     ( konštrukcia množ. G )
  6. k; k(S, |BD| )
  7.G k = {D}
  8. ABCD


Konštrukcia:





Riešenie úlohy 1 Riešenie úlohy 2 Riešenie úlohy 3 Riešenie úlohy 4 Riešenie úlohy 5 Riešenie úlohy 6 Riešenie úlohy 7 Riešenie úlohy 8 Riešenie úlohy 9 Riešenie úlohy 10 Riešenie tejto úlohy Riešenie úlohy 12 Riešenie úlohy 13 Riešenie úlohy 14 Riešenie úlohy 15

Späť na zadania