riesena16

Zostrojte ABC, ak sú dané uhly a, b a polomer vpísanej kružnice.

Riešenie tejto úlohy sme vypracovali v dvoch verziách - v jednoduchšej, ktorá využíva iba iba množinu G, a v trochu zložitejšej, ktorá využíva množinu G a vlastností uhlov. Hoci sa v niekoľkých prvých krokoch konštrukcie oba spôsoby nelíšia, rozdiel spočíva v rozbore a celkovom pohľade na riešenie úlohy.

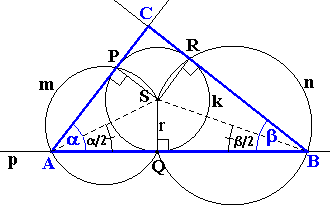
Prvá verzia využíva iba množiny "G". Zostrojte kružnicu vpísanú kružnicu. Body A, B patria priamke p, ktorá je kolmá na polomer k SQ. Teraz zostrojte dve množiny "G" "nad" SQ - jednu využitím a a druhú s b. Body A, B sú prienikom množín "G" a priamky p. Zároveň vznikli ďalšie dva body - P, R, ktoré sú prienikom k a kružníc m a n a zároveň dotykovými bodmi dotyčníc vedených bodmi A, B ku kružnici k. Bod C je prienikom a .

Náčrt prvej verzie riešenia úlohy

Rozbor:

Postup:

vrchol A:

* A p; p SQ

* A m; | SAQ | = a/2
( ?1 )

* A p m

vrchol B:

* B p; p SQ

* B n; | SBQ | = b/2
( ?2 )

* B g n

vrchol C:

* C

1. SQ; |SQ| = r

2. k; k(S; | SQ | = r )

3. p; p SQ; p Q

4. m; m = { A E²; | SAQ| = a/2 }
( ?1 )
( konštrukcia množ. G )

5. p m = { A }

6. k m = { P }

8. n; n = { B E²; | SBQ| = b/2 }
( ?2 )

9. k n = { R }
10. k p = { B }

11.

12. = { C }

13. ABC

?1,?2: Stred vpísanej kružnice je priesečník vnútorných uhlov .Preto |SAQ| = 1/2 a a |SBQ| = 1/2 b

Konštrukcia:

Druhá verzia využíva množinu "G" a vlastnosti uhlov. Prvých sedem krokov konštrukcie je rovnakých ako pri prvom postupe. Potom narysujte , kde |PSY| = a + b. Prienikom a k je R. Pretože B leží na dotyčnici ku k a R je dotykový bod, g je kolmá na SR a prechádza R. Bod B patrí prieniku g a p. Bod C je prienikom a .