Riešené príklady :

Príklad 1 :	Zostrojte graf funkcie y = 0,5x - 1,2, a potom z neho určite množinu koreňov rovnice 0,5x - 1,2 = 0 s neznámou x Î R,
Príklad 2 :	Určte rovnicu lineárnou funkciou f, pre ktorú platí : f(2) = 3, f(-3) = -7.
Príklad 3 :	Uvažujme o množine S všetkých lineárnych funkcií y = x + b, kde b Î R. Načtnite grafy štyroch funkcií, ktoré patria do S.
Príklad 4 :	Pomocou predchádzajúceho grafu funkcie f : y = 3/4 x2 sa pokúste zostrojiť graf funkcie g : y = 3/4 x2 - 3.
Príklad 5 :	Využitím grafu funkcie f : y = 3/4 x2 zostrojte graf funkcie g : y = 3/4(x + 1)2.
Príklad 6 :	Zostrojte graf funkcie g : y = 3/4(x + 1)2 - 3 pomocou grafu funkcie f : y = 3/4 x2.
Príklad 7 :	Zostrojte graf funkcie h: y =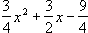
Príklad 8 :	Zistite, ktoré z daných funkcií sú párne a ktoré sú nepárne.     a)  s1 : y = 2x, x Î < -4, 5 >,     b)  s2 : y = 2 - x,     c)  s3 : y = 1 / x3,     d)  s4 : y = x2 / ( x2 + 4).
Príklad 9 :	Rozhodnite, či platí táto veta : Ak je funkcia prostá, tak je rastúca alebo klesajúca.
Príklad 10 :	Daná je funkcia g : y = x2 a podmnožina jej definičného oboru M 2 = < 0, + oo ). Riešte tieto úlohy :     a) Existuje také reálne číslo d, že pre všetky x Î M2 platí g ( x ) ł d ?     b) Existuje také reálne číslo h, že pre všetky x Î M2 platí g ( x ) Ł h ?
Príklad 11 :	Rozhodnite, či funkcia t : y = 2x + 1 je ohraničená na intervale < - oo, 0 >.
Príklad 12 :	Zistite, či funkcia h z príkladu 1 má v niektorom bode na množine M 1 = < -4, 1 > ostré maximum.

Ďalšie úlohy

Úloha 1 :	Určte rovnicou lineárnu funkciu h, pre ktorú platí :     h(3) = - 5, h(-1) = 4.
Úloha 2 :	Dokážte, že pre lineárnu funkciu f : y = ax + b platí :     a) Číslo b je hodnotou funkcie f v bode 0.     b) Pre každé dve navzájom rôzne reálne čísla x1, x2 platí :           a = [f(x2) - f(x1)] / [x2 - x1]
Úloha 3 :	Vyslovte hypotézu o tom, kedy je lineárna funkcia párna ( nepárna ) a odôvodnite ju.
Úloha 4 :	a) Dĺžka konzoly na záclonu je 3 metre, na nej je zavesených n háčikov ( 2 upevnené na krajoch, n-2 háčikov je pohyblivých). Pri vešaní záclony so šírkou z metrov vytvárame sklady, pričom šírka jedného z nich je b metrov. Vyjadrite, ako závisí z od b, n a od dĺžky konzoly.     b) Vypočítajte, akú šírku má mať záclona v prípade, keď na konzole je 20 háčikov, a pritom chceme utvoriť sklady so šírkou 0,05 metra. Podobnú úlohu riešte pre prípad, keď sa počet háčikov zväčší o 6 šírku skladov meniť nebudeme.     c) Šírka skladov má byť 0,04 metra. Akú širokú záclonu musíme kúpiť v prípade, keď na konzole je 26, 28, 30 alebo 34 háčikov.
Úloha 5 :	Daný je parametrický systém funkcií y = ax, kde parameter a Î R. Nájdite všeky funkcie z tohto systému, pre ktoré platí : Pre každé x Î < -1, 1 > patrí funkčná hodnota do intervalu ( -2, 2 ).
Úloha 6 :	Uvažujme parametrický systém funkcií y = 0,5x + b, kde parameter b Î R. Určte všetky funkcie z tohto parametrického systému, ktoré spĺňajú túto podmienku : Pre každé x Î < -3, 0 > je funkčná hodnota prvkom intervalu < -4, 7 >.
Úloha 7 :	Načrtnite graf funkcie h: y = 1,5 x2. Môžete ho využiť na zostrojenie grafu funkcie h1 : y = - 1,5 x2 ? Aká je vzájomná poloha grafov funkcií y = a x2, y = - a x2 pri danom a ą 0 ?
Úloha 8 :	Načrtnite grafy týchto funkcií :     a) y = x2 + c pre c = 0; 3; 2; - 0,5     b) y = ( x - k )2 pre k = 0; 1; 2,5; -2; -2,5     c) y = ( x - k )2 + m pre k = 1, m = 2; k = 1, m = -2; k = 1, m = 1,5     d) y = ( x - k )2 + m pre k = -2, m = 2; k = -1, m = 2; k = 0,5, m = 2
Úloha 9 :	Načrtnite grafy týchto funkcií :     a) k1 : y = x2 - 2x + 3     b) k2 : y = - x2 - 6x + 8     c) k3 : y = 2x2 + 5x - 1     d) k4 : y = - 0,5x2 + x + 2
Úloha 10 :	Určte všetky funkcie z parametrického systému funkcií y = ax2 + bx + c, kde parametre a, b, c Î R, ktorých graf má s osou x spoločný aspoň jeden bod.
Úloha 11 :	Daný je parametrický systém funkcií y = ax2, kde parametre a Î R - {0}. Určte všetky funkcie z tohto systému, pre ktoré platí : Pre každé x Î < -1, 1 > patrí funkčná hodnota do intervalu < -6, 6 >.
Úloha 12 :	Daný je parametrický systém funkcií y = x2 + c, kde parametre c Î R. Určte všetky funkcie z tohto systému, pre ktoré platí : Pre každé x Î < -2, 2 > patrí funkčná hodnota do intervalu < -3, 5 >.
Úloha 13 :	Zistite, ktoré z uvedených funkcií sú párne a ktoré sú nepárne :     a) y = x + x 3,     b) y = 1 / ( x 2 + 1 ),     c) y = 1 / x,     d) y = 1 / x 4,     e) y = x 2 + x .
Úloha 14 :	Vedeli by ste uviesť príklad funkcie, ktorá je súčasne párna i nepárna ? Existuje len jediná takáto funkcia ?
Úloha 15 :	a) Na obrázku je zostrojená časť grafu párnej funkcie m, ktorej definičný obor je < -4, 4 >. Načrtnite graf funkcie m. b) Analogickú úlohu ako v časti a) riešte pre prípad, že m je nepárna funkcia.
Úloha 16 :	Uveďte také podmnožiny definičného boru funkcie g : y = x2, na ktorých :     a) g je rastúca,     b) g je klesajúca,     c) g je prostá, ale pritom nie je ani rastúca, ani klesajúca,     d) g nie je prostá.
Úloha 17 :	Rozhodnite, ktoré z nasledujúcich funkcií sú rastúce a ktoré sú klesajúce :     a) y = 6x + 2,4     b) y = - 2x - 1     c) y = 3x2     d) y = 4
Úloha 18 :	Funkcia k je daná takto : jej definičný obor je R, pre každé racionálne číslo x platí k (x) = x, pre každé iracionálne číslo x platí k (x) = - x. Je k prostá funkcia ? Na ktorých podmnožinách definičného oboru je k rastúca, klesajúca ? Je táto funkcia rastúca alebo klesajúca na niektorom intervale ?
Úloha 19 :	Zistite, ktoré znasledujúcich funkcií sú zdola ohraničené, zhora ohraničené a ohraničené :     a) y = 0,5x + 4     b) y = - x - 2,5     c) y = - x 2     d) y = 5.
Úloha 20 :	Načrtnite graf funkcie h : y = 2x - 3. Uveďte príklady podmnožín D (h) , na ktorých o funkcii h platí :     a) je zhora ohraničená, ale nie je zdola ohraničená     b) je zdola ohraničená, ale nie je zhora ohraničená     c) nie je zhora, ani zdola ohraničená     d) je zhora i zdola ohraničená. Analogickú úlohu riešte pre funkciu k y = - 1,5x + 2.
Úloha 21 :	Dokážte, že funkcia s : y = 1 / ( x 2 + 1 ) je ohraničená.
Úloha 22 :	Rozhodnite, či platí : Funkcia h z príkladu 1 má na každom intervale, ktorý je podmnožinou D (h), v niektorom bode maximum a v niektorom bode minimum.
Úloha 23 :	Dokážte, že funkcia m : y = 2x + 1 má na intervale < -1, 3 > v bode 3 ostré maximum a v bode -1 ostré minimum.
Úloha 24 :	Rozhodnite, či funkcia y = x 2 má na intervale < -2, 2 > maximum, ostré maximum, minimum, ostré minimum.
Úloha 25 :	Načrtnite grafy týchto funkcií :        a) y = 3        b) y = x - 3        c) y = - 2x + 1        d) y = - x 2.     Zvoľte si rôzne podmnožiny definičného oboru a rozhodnite, či má na nich daná funkcia maximum, ostré maximum, minimum, ostré minimum. Nezabudnite na množinu, ktorá sa rovná definičnému oboru.