Zistite, ktoré z daných funkcií sú párne a ktoré sú nepárne.
a) s1 : y = 2x, x Î < -4, 5 >,
b) s2 : y = 2 - x,
c) s3 : y = 1 / x3,
d) s4 : y = x2 / ( x2 + 4).
Riešenie :
Pre funkciu s1 nie je splnená podmienka "ak je x prvkom definičného oboru funkcie, tak je jeho prvkom aj -x "; napríklad 5 Î D (s1), ale - 5 nepatrí D (s1). Preto s1 nie je ani párna, ani nepárna funkcia. Ak načrtneme graf funkcie s1, vidíme, že nie je súmerný ani podľa osi y, ani podľa počiatku súradnicovej sústavy.
Definičný obor funkcie s2 je R; ak teda x Î D (s2), tak aj -x Î D (s2). Napriek tomu funkcia s2 nie je ani párna, ani nepárna, pretože napríklad pre x = 1 platí s2 (1) = 1 a s2 (-1) = 3 a teda s2 (-1) <> s2 (1) a rovnako s2 (-1) <> - s2 (1). ( Môžeme si opäť načrtnúť graf funkcie s2 a na ňom overiť všetky úvahy, ktoré sme vykonali. )
Definičný obor funkcie s3 je R - {0}; pre každé reálne číslo x preto platí : Ak x Î D (s3), tak aj -x Î D (s3). Ďalej :
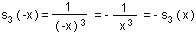
Funkcia s3 je teda nepárna.
Definičný obor funkcie s4 je R, teda :
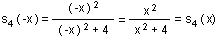
Funkcia s4 je teda párna.