Zhodné zobrazenia
S definíciou pojmu zobrazenie sa stretávajú žiaci až na strednej škole. Avšak už na základnej škole intuitívne chápu zobrazenie ako nejaké priradenie. V 6. ročníku sa stretávajú so strednovou a osovou súmernosťou, osvoja si pojmy vzor a obraz i základné vlastnosti oboch súmerností, riešia jednoduché konštrukčné úlohy a naučia sa formálne zapisovať zobrazenie ako priradenie X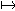 X' (bodu X priradíme bod X').
X' (bodu X priradíme bod X').
Stredová súmernosť
Definícia: Stredovou súmernosťou S danou stredom S je zhodné zobrazenie v rovine, ktoré bodu X=S priradí bod X'=S a každému X S priradí bod X' tak, že platí:
S priradí bod X' tak, že platí:
• X, X', S ležia na jednej priamke,
• |XS|=|X'S|, pričom X' X.
X.
Zapisujeme SS(X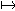 X').
X').
Vlastnosti
- stredová súmernosť je svojim stredom jednoznačne určená (to znamená, že po zostrojení stredu môžeme v tejto súmernosti každému bodu X roviny priradiť práve jeden obraz X'),
- má jediný samodružný bod, a to stred S,
- samodružné priamky stredovej súmernosti sú všetky priamky prechádzajúce stredom S,
- stredová súmernosť zobrazí každú priamku do priamky s ňou rovnobežnej,
- stredová súmernosť zobrazí uhol do uhla s ním zhodného,
- stredovú súmernosť možno rozložiť na dve osové súmernosti, ktorých osi sú dve ľubovoľné navzájom kolmé priamky prechádzajúce stredom S danej súmernosti,
- každé dva body roviny sú vzorom a obrazom v práve jednej stredovej súmernosti, ktorej stredom S je stred úsečky danej týmito dvoma bodmi.
Osová súmernosť
Definícia: Osovou súmernosťou O danou osou o je zhodné zobrazenie v rovine, ktoré každému bodu X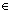 o priradí bod X'=X a každému bodu X
o priradí bod X'=X a každému bodu X o priradí bo X' tak, že platí:
o priradí bo X' tak, že platí:
• X' leží v opačnej polrovine ako bod X vzhľadom na os o,
• úsečka XX' je kolmá na os o,
• body X, X' sú od osi o rovnako vzdialené.
Zapisujeme Oo(X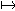 X').
X').
Vlastnosti
- osová súmernosť je osou o súmernosti jednoznačne daná (to znamená, že po zostrojení osi súmernosti môžeme v tejto súmernosti každému bodu X roviny priradiť jeho obraz X'),
- samodružné body sú všetky body osi o,
- samodružné priamky sú os o a všetky priamky kolmé na os o,
- obrazom každej priamky p rovnobežnej s osou o súmernosti je priamka p' rovnobežná s osou o,
- obrazom každej priamky q rôznobežnej s osou o súmernosti, je priamka q' pretínajúca primaku q v bode osi o,
- obrazom uhla v osovej súmernosti je uhol s ním zhodný,
- každé dva body roviny sú vzorom a obrazom v práve jednej osovej súmernosti, ktorej osou o je os úsečky danej týmito dvoma bodmi.
PRÍKLADY NA ZHODNÉ ZOBRAZENIE
- Daná je kružnica k(S;r) a jej vonkajší bod A. Zostrojte dotyčnice kružnice k s jej dotyčnicou prechádzajúcou bodom A bez použitia Talesovej kružnice. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daná jeho ťažnica ta a jeho výšky vb, vc. RIEŠENIE
- Zostrojte trojuholník ABC, ak poznáte a+b, va, c. RIEŠENIE
- Zostrojte trojuholník ABC, ak poznáte a, b,
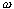 =
=  -
-  (
( je uhol BAC,
je uhol BAC,  je uhol ABC,
je uhol ABC,  >
>  , a > b). RIEŠENIE
, a > b). RIEŠENIE
- Daná je priamka MN a dve rôzne kružnice k1, k2 ležiace v tej istej polrovine vzhľadom na priamku MN, ktoré s ňou nemajú spoločný bod. Na priamke MN zostrojte taký bod X, aby dotyčnice vedené z bodu X ku kružniciam k1, k2 zvierali s priamkou MN zhodné uhly. RIEŠENIE
- Zostrojte spoločné dotyčnice dvoch kružníc k1(S1; r1), k2(S2; r2), ktoré nemajú spoločný bod a jedna neleží vo vnútri druhej, pričom r1
 r2 bez použitia rovnoľahlosti. RIEŠENIE
r2 bez použitia rovnoľahlosti. RIEŠENIE
- Zostrojte rovnoramenný trojuholník ABC, ktorého vrcholy ležia na troch sústredných kružniciach k1(S; r1), k2(S; r2), k3(S; r3). RIEŠENIE
 X' (bodu X priradíme bod X').
X' (bodu X priradíme bod X').
 X' (bodu X priradíme bod X').
X' (bodu X priradíme bod X').
 S priradí bod X' tak, že platí:
S priradí bod X' tak, že platí:
 X.
X.
 X').
X').
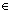 o priradí bod X'=X a každému bodu X
o priradí bod X'=X a každému bodu X o priradí bo X' tak, že platí:
o priradí bo X' tak, že platí:
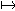 X').
X').
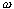 =
=  -
-  (
( je uhol BAC,
je uhol BAC,  je uhol ABC,
je uhol ABC,  >
>  , a > b). RIEŠENIE
, a > b). RIEŠENIE
 r2 bez použitia rovnoľahlosti. RIEŠENIE
r2 bez použitia rovnoľahlosti. RIEŠENIE