Rovnoľahlosť
S pojmom rovnoľahlosť sa žiaci stretávajú prvýkrát až na strednej škole. V gymnáziu je toto učivo zaradené do prvého ročníka.
Podobne, ako je to pri zhodných zobrazeniach, aj rovnoľahlosť je zobrazenie s určitými špecifickými vlastnosťami. Daný je pevný bod S, ktorý nazveme stredom rovnoľahlosti a reálne číslo h (zvyčajne sa požaduje, aby h 0, h
0, h 1), ktoré nazveme koeficientom rovnoľahlosti. Každému bodu roviny X priradíme X' tak, aby |S'| = |h|.|SX|, a aby bod X' ležal na polpriamke SX, ak je h>0, a na polpriamke opačnej k polpriamke SX, ak je h<0. Takže rovnoľahlosť si môžeme zadefinovať takto :
1), ktoré nazveme koeficientom rovnoľahlosti. Každému bodu roviny X priradíme X' tak, aby |S'| = |h|.|SX|, a aby bod X' ležal na polpriamke SX, ak je h>0, a na polpriamke opačnej k polpriamke SX, ak je h<0. Takže rovnoľahlosť si môžeme zadefinovať takto :
Definícia : Rovnoľahlosť (homotetia) so stredom S a koeficientom h 0 je zobrazenie, ktoré priraďuje bodu X = S bod X ' tak, že platí |SX'| = |h|.|SX|, pričom X' leží pre h>0 na polpriamke SX a pre h<0 na polriamke opačnej k SX. Označme HS(S,h).
0 je zobrazenie, ktoré priraďuje bodu X = S bod X ' tak, že platí |SX'| = |h|.|SX|, pričom X' leží pre h>0 na polpriamke SX a pre h<0 na polriamke opačnej k SX. Označme HS(S,h).
Na konštrukčné účely sa rovnľahlosť určuje obyčajne svojim stredom a jednou dvojicou bodov vzor-obraz : HS(A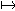 A' ). Všetky tri body sú pritom rôzne a ležia na je jednej priamke.
A' ). Všetky tri body sú pritom rôzne a ležia na je jednej priamke.
Vlastnosti rovnoľahlosti
- rovnoľahlosť zobrazuje každú priamku na priamku s ňou rovnobežnú,
- rovnoľahlosť zobrazuje každú úsečku XY na úsečku X'Y' , pre ktorú platí : X'Y' || XY, |SX'| = |h|.|SX|,
- každé dve rovnobežné úsečky, ktoré nie sú zhodné, sú rovnoľahlé dvoma spôsobmi (existujú práve dve rovnoľahlosti, ktoré jednu z nich zobrazia na druhú),
- každé dve kružnice sú rovnoľahlé dvoma spôsobmi,
- každé dva rovnoľahlé trojuholíky sú podobné,
- nie každé dva podobné trojuhololníky sú rovnoľahlé.
Konštrukčné a iné úlohy s využitím rovnoľahlosti
Rovnoľahlosť sa zvyčajne používa
- pri hľadaní spoločných dotyčníc dvoch kružníc,
- pri hľadaní množiny bodov s danou vlastnosťou,
- v úlohách, v ktorých vystupuje pomer.
V konštrukčných úlohách môžeme rovnoľahlosť použiť tak, že najprv zostrojíme útvar rovnoľahlý s hľadaným útvarom a potom podľa ďalších podmienok zostrojíme hľadaný útvar. (Spoločné dotyčnice dvoch kružníc sa dajú nájsť aj bez použitia rovnoľahlosti)
PRÍKLADY NA ROVNOĽAHLOSŤ
- K danému trojuholníku ABC zostrojte rovnoľahlé trojuholníky A1B1C1, A2B2C2 v rovnoľahlosti H danej stredom S ležiaceho mimo trojuholníka ABC a koeficientom:
- h1=3/5,
- h2= -3/5. RIEŠENIE
- Určte šírku rieky, ktorej druhý breh je neprístupný. RIEŠENIE
- Narysujte všetky spoločné dotyčnice k dvom rôznym kružniciam, ktoré nemajú spoločný žiaden bod a jedna neleží vo vnútri druhej. RIEŠENIE
- Do daného konvexného kruhového výseku KSL vpíšte štvorec ABCD tak, aby trojuholník ABC bol rovnoramenný so základňou AB. RIEŠENIE
- Zostrojte kružnicu dotýkajúcu sa danej kružnice m(O; r) a danej priamky p v bode T (Pappova úloha). RIEŠENIE
- Dané sú dve rôznobežky a, b a kružnica k(K; r), ktorá sa nedotýka žiadnej z nich. Zostrojte kružnicu l, ktorá sa dotýka súčastne a, b, k. RIEŠENIE
 0, h
0, h 1), ktoré nazveme koeficientom rovnoľahlosti. Každému bodu roviny X priradíme X' tak, aby |S'| = |h|.|SX|, a aby bod X' ležal na polpriamke SX, ak je h>0, a na polpriamke opačnej k polpriamke SX, ak je h<0. Takže rovnoľahlosť si môžeme zadefinovať takto :
1), ktoré nazveme koeficientom rovnoľahlosti. Každému bodu roviny X priradíme X' tak, aby |S'| = |h|.|SX|, a aby bod X' ležal na polpriamke SX, ak je h>0, a na polpriamke opačnej k polpriamke SX, ak je h<0. Takže rovnoľahlosť si môžeme zadefinovať takto :
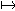 A' ). Všetky tri body sú pritom rôzne a ležia na je jednej priamke.
A' ). Všetky tri body sú pritom rôzne a ležia na je jednej priamke.