Konštrukčné úlohy trojuholíkov
Cieľom konštrukčnej úlohy je z daných bodov narysovať požadovaný útvar. Riešiť konštrukčnú úlohu znamená podľa platných viet odvodiť a doplniť dané prvky novými tak, aby sme dospeli k hľadanému útvaru. Pritom používame tzv. základné konštrukcie, a to :
K1: Ak sú dané dva rôzne body A, B, potom považujeme priamku AB za zostrojenú.
K2: Ak je daný bod S a úsečka dĺžky r, potom považujeme kružnicu k(S;r) za zostrojenú.
K3: Ak sú dané dve rôznobežky a,b ich prisečník X považujeme za zostrojený.
K4: Ak je daná kružnica k a jej sečnica m, potom považujeme ich priesečníky X,Y (X Y) za zostrojené.
Y) za zostrojené.
K5: Ak sú dané dve kružnice k1 a k2, o ktorých vieme, že sa pretínajú, potom považujeme ich priesečníky za zostrojené.
Konštrukcie uskutočnené pomocou základných konštrukcií K1 až K5 nazývame euklidovskými konštrukciami a pri ich grafckom uskutočňovaní vystačíme s kružidlom a pravítkom.
Každá konštrukčná úloha, ak má byť úplná, musí obsahovať štyri časti :
- rozbor (analýzu),
- konštrukciu,
- dôkaz správnosti konštrukcie,
- diskusiu.
Vety o zhodnosti torjuholíkov
(sss) Každé dva trojuholníky, ktoré sa zhodujú vo všetkých troch stranách, sú zhodné.
(sus) Každé dva trojuholníky, ktoré sa zhodujú v dvoch stranách a uhle nimi zovretom, sú zhodné
(usu) Každé dva trojuholníky, ktoré sa zhodujú v jednej strane a dvoch uhloch k nej priľahlých, sú zhodné,
(suu) Každé dva trojuholníky, ktoré sa zhodujú v dvoch uhloch a strane oproti jednému z nich, sú zhodné
(ssu) Každé dva trojuholníky, ktoré sa zhodujú v dvoch stranách a v uhle oproti väčšej z nich, sú zhodné
Vety o vzťahoch medzi stranami a uhlami v tom istom trojuholíku
- proti zhodným stranám ležia zhodné uhly,
- proti zhodným uhlom ležia zhodné strany,
- proti väčšej strane leží väčší uhol,
- proti väčšiemu uhlu leží väčšia strana,
- súčet dvoch strán je väčší ako tretia strana,
- reozdiel dvoch srtán je väčší ako tretia strana,
- v každom trojuholíku je vonkajší uhol pri jednom vrchole väčší ako vnútorný uhol pri ktoromkoľvek ďalšom vrchole,
- v každom trojuholíku sa vonkajší uhol pri jednom vrchole rovná súčtu vnútorných uhlov prizvyšných dvoch vrcholoch,
- v každom trojuholíku sa súčet vnútorných uhlov rovná priamemu uhlu.
PRÍKLADY NA KONŠTRUKCIU TROJUHOLNÍKOV
- Zostrojte trojuholník ABC, ak poznáte
 ,
,  a výšku vc. RIEŠENIE
a výšku vc. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daná strana a, výšky vb, vc (vb, vc ležia v tej istej polrovine vzhľadom na priamku BC, vb
 a
a vc). RIEŠENIE
vc). RIEŠENIE
- Zostrojte trojuholník ABC, ak je daný bod M, ktorý je pätou kolmice z vrcholu A na stranu BC; bod N, ktorý je pätou kolmice z vrcholu B na stranu AC a priamka p, na ktorej leží strana AB. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daný polomer r opísanej kružnice, výška vc a ťažnica tc. RIEŠENIE
- Zostrojte trojuholník ABC, ak je daný jeho obvod a + b + c a uhly
 a
a 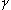 . RIEŠENIE
. RIEŠENIE
- Zostrojte rovnoramenný trojuholník ABC vpísaný do danej kružnice k(S; r), ak je daný súčet a + v veľkosti jeho základne a príslušnej výšky. RIEŠENIE
 Y) za zostrojené.
Y) za zostrojené. ,
,  a výšku vc.
a výšku vc. 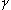 .
.