 |
Na kružnici sú dané dve trojice bodov A, X, B a C, Y, D
tak, že |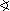 AXB| = | AXB| = |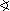 CYD|. Dokážte, že |AB| = |CD|. CYD|. Dokážte, že |AB| = |CD|. |

|
Bodom A kružnice k(S; r) veďte
priemer AB a tetivu AC = r. Dokážte, že 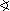 ABC
= 30o. ABC
= 30o. |
 |
V kružnici je narysovaný ľubovoľný
priemer AB a dve zhodné tetivy |AC|=|AD|. Dokážte, že aj tetivy BC,
BD sú zhodné. |

|
Dokážte, že os dvoch pretínajúcich
sa kružníc k1(S1; r1) a k2(S2;
r2) je kolmá na spoločnú tetivu týchto kružníc a poltí
ju. |
 |
Kružnice k1(S1;
r1) a k2(S2; r2) sú sústredné.
Tetiva AB kružnice k1 sa dotýka kružnice k2 v
bode T. Dokážte, že dotykový bod T je stredom úsečky AB. |
 |
Dokážte, že vonkajší uhol
tetivového štvoruholníka je zhodný s vnútorným uhlom pri protiľahlom
vrchole. |


