Pri tomto dôkaze sme
použili dve dvojice trojuholníkov: 
ABD, ABC a
ASD, ASC.
ABD
a ABC:
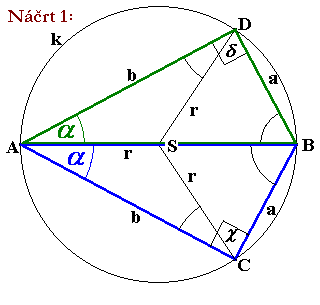
Strana AB je zároveň priemerom kružnice. Body C, D patria Talesovej kružnici nad
priemerom AB, preto je pri vrcholoch C, D uhol c = d = 90o.Tieto
trojuholníky sa zároveň zhodujú
v strane b = |AD| = |AC|, strane c = |AB| = 2r a v uhle c = d
= |
ABD|
= |ACB| =
90o.
ASD
a ASC:
Z Náčrtu 2 (
kliknite na náčrt ) vyplýva, že ASD
ASC,
pretože sa zhodujú vo všetkých troch stranách. Z toho vyplýva, že sa
zhodujú aj vo všetkých uhloch.
Pre nás je podstatná zhodnosť uhlov |DAS|
= |SAC| = a.
Ak sa teraz vrátime späť do Náčrtu 1, vidíme, že ABD
a ABC sa zhodujú
v dvoch stranách (|AD| = |AC| = b; |AB| = 2r;) a v uhle nimi zovretom (|DAS|
= |SAC| = a),
preto sa musia zhodovať aj v tretej. Platí to, čo bolo treba dokázať, teda že:
