Tetivový štvoruholník

Tetivový štvoruholník je štvoruholník, ktorého všetky štyri strany sú tetivami kružnice. Zároveň je to každý štvoruholník, ktorému možno opísať kružnicu.
Najvýznamnejšou vlastnosťou tetivového štvoruholníka je, že súčet veľkostí protiľahlých uhlov je 180^o.

Toto tvrdenie dokážeme tak, že dokážeme nasledujúce implikácie:

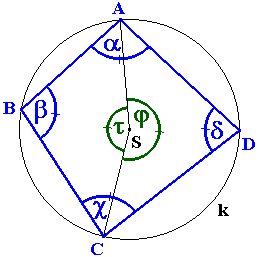
Dôkaz prvej implikácie

I. Ak je 4-uholník tetivový, potom súčet veľkostí protiľahlých uhlov je 180^o.

Z vety o vzájomnej závislosti stredového a obvodového uhla vyplýva:

2b = j 2d = t

Z náčrtu zároveň vyplýva, že:

j + t = 360^o

Preto po dosadení:

2b	+	2d	= 360^o
2( b	+	d )	= 360^o	/:2
b	+	d	= 180^o

Analogicky dokážeme, že a + c = 180^o.

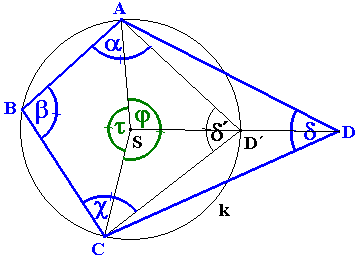
Dôkaz druhej implikácie

II. Ak súčet veľkostí protiľahlých uhlov je 180^o, potom 4-uholník je tetivový.

Dôkaz implikácie uskutočníme napr. sporom. Teda predpokladajme, že:
Nech súčet veľkostí protiľahlých uhlov je 180^o a zároveň 4-uholník nie je tetivový.

Úsečka SD pretla kružnicu k v bode D´. Štvoruholník ABCD´ je tetivový, teda podľa predchádzajúceho platí:

b + = 180^o.

Z daných rovností

b + = 180^o b + d = 180^o

vyplýva, že d = 180^o, preto aj D = D´, čo je v spore s predpokladom, že 4-uholník ABCD nie je tetivový. Preto platí pôvodné tvrdenie.

Späť na zadania