Vychádzali sme z rovnoramenného 
ABS, pre ktorý platí:
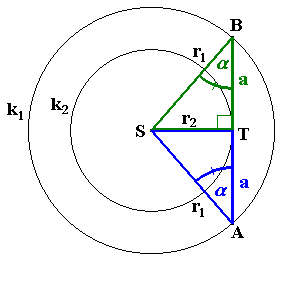
Kružnice k1(S1; r1) a k2(S2; r2) sú sústredné. Tetiva AB kružnice k1 sa dotýka kružnice k2 v bode T.
Dokážte, že dotykový bod T je stredom úsečky AB.
Vychádzali sme z rovnoramenného
ABS, pre ktorý platí:
|SA| = |SB| =
r 
|
SAT| = |SBT|.
AB je dotyčnica k2,
je kolmá na polomer k2, preto |ST| = r2 
AB. ST je zároveň výškou
ABS a pretože tento trojuholník je rovnoramenný, výška na AB delí
ABS na dva trojuholníky:
STB
a STA:
|STB|
= |STA| =
90o
|SAT|
= |SBT| = a
|AST|
= |BST| =
180o - ( 90o + a ) = 90o - a
Trojuholníky sa zhodujú v dvoch stranách ( SB a ST ) a uhle nimi zovretom ( a ), preto sa zhodujú aj v tretej strane:
|AT|
= |BT| = |AB| / 2
