Dôkaz vety o vzájomnom vzťahu

stredového a obvodového uhla v kružnici

Dôkaz tejto vety sa opiera o vlastnosti vonkajších a vnútorných uhlov trojuholníka, rovnoramenných a pravouhlých trojuholníkov. Je potrebné ho vykonať pre všetky možné vzájomné polohy ramien stredového a obvodového uhla.

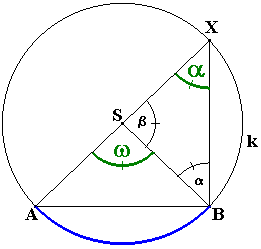
SBX je rovnoramenný ( lebo |SX| = |SB| = r ). Preto |SXB| = |SBX| = a. Veľkosť tretieho uhla je preto b = 180^o - 2a. Uhol w je susedným uhlom k b, preto:

b = 180^o - 2a w = 180^o - b

w = 180^o - b

w = 180^o - ( 180^o - 2a )

w = 2a

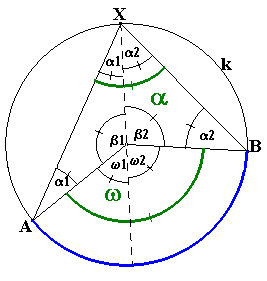Druhá vzájomná poloha ramien stredového a obvodového uhla Vychádzame z dvoch ramien rovnoramenných trojuholníkov ASX a BSX. Vypočítame uhly w1 a w2, ktorých súčtom je w:

b1 = 180^o - 2a1
w1 = 180^o - b1
w1 = 180^o - ( 180^o - 2a1 )
w1 = 2a1

b2= 180^o - 2a2
w2 = 180^o - b2
w2 = 180^o - ( 180^o - 2a2 )
w2 = 2a2

w = w1 + w2
w = 2a1 + 2a2
w = 2( a1 + a2 )

w = 2a

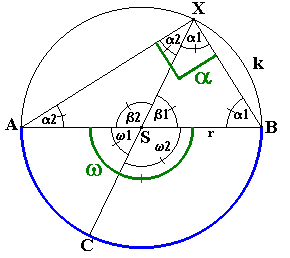
Tretia vzájomná poloha stredového a obvodového uhla v kružnici

Vychádzame z dvoch rovnoramenných trojuholníkov BSX a ASX:

b1 = 180^o - 2a1

b2 = 180^o - 2a2

w = w1 + w2
w = 2a1 + 2w2
w = 2( a1 + a2 )

w = 2a

w1 = 180^o - b2 = 180^o - ( 180^o - 2a2 ) = 2a2
w2 = 180^o - b1 = 180^o - ( 180^o - 2a1 ) = 2a1

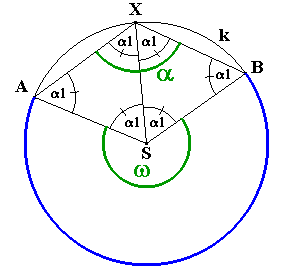Štvrtá vzájomná poloha ramien stredového a obvodového uhla

Vychádzame z dvoch rovnostranných trojuholníkov

ASX a

BSX.

|AS| = |AX| = |BS| = |BX| = |XS| = r.

Pretože trojuholníky sú rovnostranné, všetky uhly sú zhodné, teda platí:

a1 = 180^o / 3 = 60^o

a = 2a1 = 120^o

w = 360^o- 2a1 = 360^o - a = 240^o

w = 2a

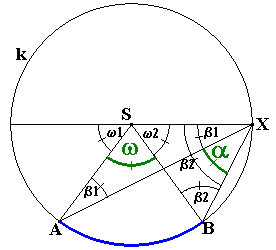Piata vzájomná poloha ramien stredového a obvodového uhla Použijeme AXS a BXS.

w1 = 180^o - ( w + w2 ) =
= 180^o - ( 180^o - 2b1 ) =
= 2b1
w2 = 180^o - 2b2
a = b2 - b1

w = 180^o - ( w1 + w2 )
w = 180^o - ( 2b1 + 180^o - 2b2 )
w = 2b2 - 2b1
w = 2( b2 - b1 )

w = 2a

Späť na zadania