y = ax2 + bx + c, kde a je reálne číslo rôzne od nuly, b, c sú ľubovoľné reálne čísla. |
|
Začneme funkciou f: y = x2. Grafom tejto funkcie je parabola: |
|
1. Obor hodnôt je <0, +Ą>. |
| Načrtneme teraz graf funkcie f: y = x2, a potom v tej istej sústave zakreslíme graf funkcie f1: y = 1/3 x2. Využijeme pritom, že pre každé x Î R platí: f1(x) = 1/3 f(x)(pozri obrázok). |
|
Analogicky postupujme pri zostrojovaní grafov funkcií y = 2x2, y = 0,5x2, y = -x2, y = -1/4x2(pozri obrázok). |
| Na základe záverov o vlastnostiach funkcie y = x2 a využitím získaných grafov funkcií z obrázka môžeme vysloviť hypotézy o vlastnostiach kvadratických funkcií z parametrického systému y = ax2. |
|
Vlastnosti kvadratickej funkcie.
|
|
Príklady :
| |
 Príklad 1 :
Príklad 1 : | Pomocou predchádzajúceho grafu funkcie f : y = 3/4 x2 sa pokúste zostrojiť graf funkcie g : y = 3/4 x2 - 3. |
 Príklad 2 :
Príklad 2 : | Využitím grafu funkcie f : y = 3/4 x2 zostrojte graf funkcie g : y = 3/4(x + 1)2. |
 Príklad 3 :
Príklad 3 : | Zostrojte graf funkcie g : y = 3/4(x + 1)2 - 3 pomocou grafu funkcie f : y = 3/4 x2. |
 Príklad 4 :
Príklad 4 : | Zostrojte graf funkcie h: y = 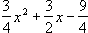 |
| Ďalšie úlohy |