V pravouhlom trojuholníku ABC, v ktorom pravým uhlom je uhol g, platí :
c2 = a2 + b2
Druhá mocnina veľkosti prepony pravouhlého trojuholníka sa rovná súčut druhých mocnín veľkostí odvesien tohto trojuholníka.
Ako dôkaz Pytagorovej vety stačí použiť rovnosť : c2 = a2 + b2 - 2 a b cos g z Kosínusovej vety a dosadiť g = p / 2 .
Dôkaz obrátenej Pytagorovej vety :
Dôkaz urobíme sporom : Predpokladajme, že pre dĺžky a, b, c strán trojuholníka ABC platí : c2 = a2 + b2, pričom uhol ACB oproti strane c nie je pravý.
Vieme zostrojiť trojuholník ABC1 taký, aby platilo :
|AC1| = |AC|,
|uhol AC1B| = 90o
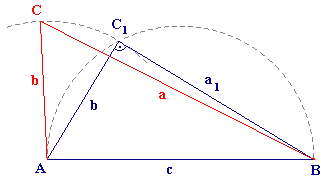
a12 + b2 = a2 + b2
Odčítame b2 : a12 = a2
Keďže a1, a sú kladné, dostávame : a1 = a - trojuholníky ABC, ABC1 sú zhodné podľa sss, ale nezhodujú sa v zodpovedajúcich si vnútorných uhloch ACB, AC1B - spor. Predpoklad, že uhol ACB nie je pravý, je teda nesprávny. To znamená, že ak pre strany a, b, c trojuholníka ABC platí c2 = a2 + b2, je tento trojuholník pravouhlý s pravým uhlom oproti strane c, čo bolo treba dokázať.
Dôkaz pomocou podobnosti :
Použijeme tvrdenia z dôkazu Euklidovej vety o odvesne :
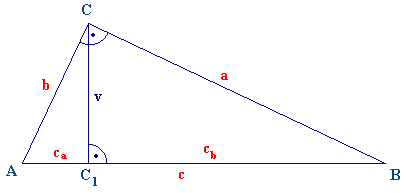
a2 + b2 = c.ca + c.cb = c ( ca + cb ) = c2 - > c2 = a2 + b2.
