Kosínusová veta


V ľubovoľnom trojuholníku ABC platí :

             a2 = b2 + c2 - 2 b c cos a
             b2 = a2 + c2 - 2 a c cos b
             c2 = a2 + b2 - 2 a b cos g

Dôkaz :

       Dôkaz obmedzíme najprv na trojuholníky, v ktorých ani jeden z uhlov b, g nie je pravý. S použitím nasledovných náčrtov dostávame :




             a = |BVa| + |VaC| = c cos b + b cos g ,
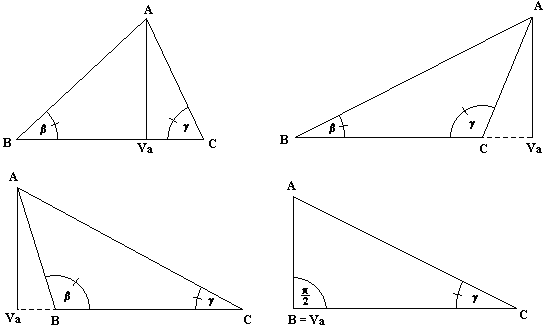
             a = |BVa| - |CVa| = c cos b - b cos ( p - g ) = c cos b + b cos g ,
             a = |VaC| - |VaB| = b cos g - c cos ( p - b ) = c cos b + b cos g .

       Tu sme použili vzťah cos p - j ) = - cos j. Vo všetkých troch prípadoch však dostávame rovnaký výsledok a = c cos b + b cos g, ktorý naviac, ako je vidno z štvrtého náčrtu, platí i v prípade, ak niektorý z uhlov b, g je pravý. Po umocnení na druhú dostávame :
             a2 = ( b cos g + c cos b )2 ,
             a2 = b2 cos2 g + c2 cos2 b + 2 b c cos b cos g ,
             a2 = b2 ( 1 - sin2 g ) + c2 ( 1 - sin2 b ) + 2 b c cos b cos g ,
             a2 = b2 + c2 - b2 sin2 g - c2 sin2 b + 2 b c cos b cos g .

       Jeden zo vzorcov sínusovej vety : b sin g = c sin b môžeme napísať aj ako :
b sin g - c sin b = 0. Pri jeho umocnení na druhú dostávame :

             b2 sin2 g + c2 sin2 b - 2 b c cos b cos g = 0 ,

čo umožňuje v predchádzajúcom výpočte pokračovať takto :

             a2 = b2 + c2 + 2 b c ( cos b cos g - sin b sin g ) ,
             a2 = b2 + c2 + 2 b c cos ( b + g ) ,
             a2 = b2 + c2 + 2 b c cos ( p + a ) ,
             a2 = b2 + c2 - 2 b c cos a .

Tým je prvá rovnosť dokázaná. Ostatné dve rovnosti sa dajú dokázať úplne analogicky.