Príklad č.6
Daná je úsečka AB, ďalej polrovina ABM a dutý uhol 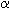 . Nájdite množinu všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=
. Nájdite množinu všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=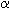 .
.
ROZBOR:
- Množina všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=
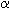 , je istý oblúk AB bez krajných bodov A,B.
, je istý oblúk AB bez krajných bodov A,B.
KONŠTRUKCIA:
- V polrovine opačnej k polrovine ABM, zostrojíme úsekový uhol BAQ=
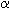 .
.
- zostrojíme priamku q kolmú na AQ, ktorá prechádza bodom A a označíme p os úsečky AB.
- Priesečník S priamok p, q je stred hľadaného oblúku AB; polomer oblúku je SA.

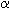 . Nájdite množinu všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=
. Nájdite množinu všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=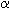 .
. 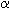 . Nájdite množinu všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=
. Nájdite množinu všetkých bodov X, ktoré ležia vo zvolenej polrovine ABM a platí pre ne, že uhol AXB=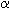 .
. 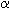 , je istý oblúk AB bez krajných bodov A,B.
, je istý oblúk AB bez krajných bodov A,B. 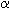 .
.