| Nepriama úmernosť | Lineárne lomená funkcia |
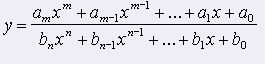 (1) (1)kde m, n sú celé nezáporné čísla, am, ..., a0; bn, ..., b0 sú reálne čísla, bn ą 0. |
| Tieto funkcie definované na množine všetkých takých x Î R, ktoré nie sú koreňmi rovnice: bnxn + bn - 1xn - 1 + ... + b1x + b0 = 0 Špeciálnym prípadom racionálnych funkcií sú polynomické funkcie; sú dané rovnicou (1), v ktorej platí: n = 0, b0 = 1. Ide teda o funkcie, ktoré môžeme vyjadriť v tvare: y = amxm + bm - 1xm - 1 + ... + a1x + a0. Definičným oborom každej polynomickej funkcie je množina R všetkých reálnych čísel. Príkladom polynomickej funkcie je kvadratická funkcia, príkladom racionálnej funkcie, ktorá nie je polynomická, je nepriama úmernosť. |