Dôkaz Talesovej vety



Máme dokázať, že množina bodov, z ktorých vidíme úsečku AB pod pravým uhlom, je kružnica k(S;r ) okrem bodov A, B, pre ktorú je daná úsečka priemerom.


 Nech t je kružnica so stredom S v strede úsečky AB a polomerom r = |AB| / 2.


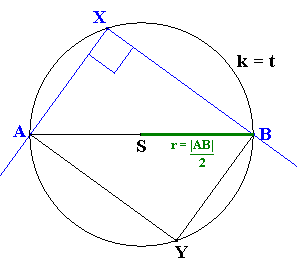
Dôkaz, že X patrí kružnici k



Nech X je vrcholom pravého uhla AXB. Dokážeme, že X t:

Pravouhlý AXB doplníme na AXBY, ktorému môžeme opísať kružnicu k(S; r ). Polomerom kružnice je úsečka r = |SA| = |SB| = |AB| / 2, kde S je stredom úsečky AB.

Z toho vyplýva, že k je totožná s kružnicou t, pretože aj tá je zostrojená z bodu S, ktorý je stredom AB, a má polomer r = |AB| / 2  

S = A B k = t X t


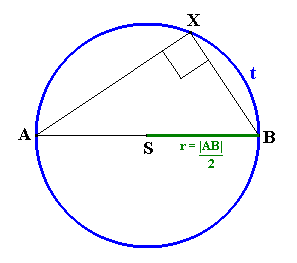
Dôkaz, že uhol AXB je pravý

Nech X t       X A      X B. Dokážeme, že AXB je pravý:

AXB je obvodovým uhlom k ASB, ktorý je priamy    AXB je pravý:

AXB =  1/2 ASB = 180o / 2 = 90o


Z toho všetkého vyplýva, že:

Množinou všetkých bodov, z ktorých úsečku AB vidíme pod uhlom 90o je kružnica t, pre ktorú je úsečka AB priemerom, okrem bodov A, B.
( Talesova veta )