Sínusová veta

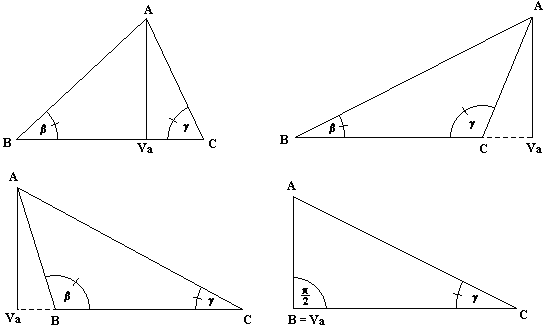
V ľubovoľnom trojuholníku ABC platí :              a sin b = c sin a              b sin g = b sin b              c sin a = a sin g Dôkaz :        Vychádzame z prvých troch náčrtov :        V jednotlivých prípadoch dostávame        sin b = va / c,        sin b = va / c,        sin ( p - b ) = va / c.        Pretože však ( p - b ) = sin b, dostávame vo všetkých troch prípadoch rovnaký výsledok va = b sin g. V prípade, že b = p / 2 však rovnako platí va = c sin b = c ( obrázok číslo 4 ).        Platí teda vždy va = c sin b. Celkom analogickým postupom dostaneme va = b sin g. Z oboch týchto rovností dostávame b * sin g = c * sin b, čo je jedna z rovností v tvrdení vety. Ostatné dve získame analogickým postupom.

---

---