Trojuholník s parametrami : uhol a, ťažnica tb, ťažnica tc


Rozbor :

      Bod A leží na kružnicovom oblúku kružnice k, z ktorého je vidieť úsečku BTb pod uhlom a. Bod Tc leží na
      oblúku k', ktorý vznikne ako obraz oblúku k pri rovnoľahlosti so stredom B a koeficientom 1/2.

Konštrukcia :

      1. Úsečka BTb = tb.
      2. Množina bodov v rovine, z ktorých je vidieť úsečku BTb pod uhlom a
      (oblúk kružnice k, viď úlohu 4, bod 3), v príslušnej polrovine vyťatej priamkou BTb.
      3. Obraz k' oblúku kružnice k v rovnoľahlosti h, h = (B; 1/2).
      4. T Î BTb tak, že |BT| = 2 |TTb|.
      5. Kružnica l = (T; 1/3 tc).
      6. l Ç k' = Tc.
      7. BTc Ç k = A.
      8. Doplníme D ABC.


Podmienky riešiteľnosti :

   .

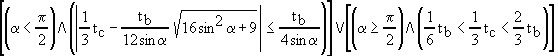Počet riešení :

   ,
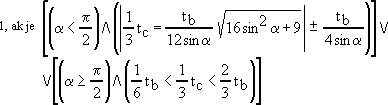  2. ak je .
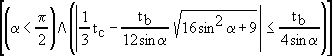