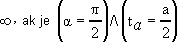| Zavedieme toto označenie: | |
| x = a2, | (1) |
| u = b2 + c2 - a2, | (2) |
| v = 2bc | (3) |
| a vzťah | |
 |
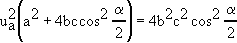(4) |
| ktorý podľa označenia (1), (2) a (3) prepíšeme na tvar: | |
 |
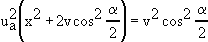(5) |
| ďalej potom platí: | |
| u = v cosa | (6) |
| x + 2u = 4ta2 | (7) |
| V sústave rovníc (5), (6) a (7) s neznámymi x, u, v je iba rovnica (5) kvadratická. Jej riešením získame hodnotu x = a2, teda i dĺžku a. | |
Konštrukcia : 1. Úsečka BC, |BC| = a. 2. Množina všetkých bodov, z ktorých vidíme úsečku BC pod uhlom a ( oblúk križnice k1), a to v príslušnej polrovine vyťatej priamkou BC (viď úlohu 4, bod 3). 3. Kružnica k2 = (Ta; ta) 4. k1 Ç k2 = A. | |
Podmienky riešiteľnosti : | |
 | |
| Počet riešení :  , .
 | |
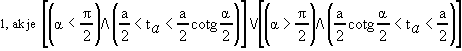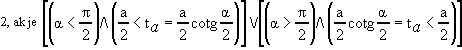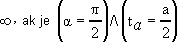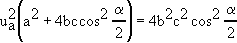
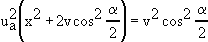
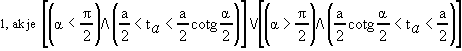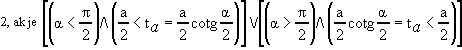