Trojuholník s parametrami: výška va,polomer r,polomer r
Rozbor :
|
Použitím substitúcie:
u = b + c
v = b - c
|
ďalej požitím vzťahov:
(a + b + c)r = ava
abc = 2rr(a + b + c) |
| po vylúčení a dospejeme k sústave: |
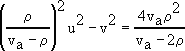 |
(1) |
| u2 - v2 = 8rva |
(2) |
| Odtiaľ ľahko vypočítame u, v resp. b, c. |
| Táto úloha sa takto prevedie na úlohu s parametrami b, c, r. |
Konštrukcia:
1. Úsečka AC, |AC| = b.
2. Kružnica k1 prechádzajúca bodmi B, C s polomerom r
3. Kružnica k2 = (C; b).
4. k1 Ç k2 = B.
|
Podmienky riešiteľnosti :
|
| [(b Ł 2r) /\ (c < 2r)] \/ [(b < 2r) /\ (c Ł 2r)] |
Počet riešení :
1, ak je (b = 2r) \/ (c = 2r) \/ (b = c < 2r),
2, ak je (b < 2r) \/ (c < 2r) \/ (b ą c). |