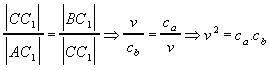Euklidove vety
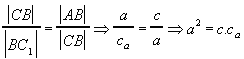
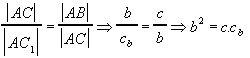
Euklidova veta o odvesne Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdlžníka zostrojeného z prepony a úseku na prepone priľahlého k odvesne. Pre jednotlivé odvesny trojuholníka teda platí : a² = c.c_a b² = c.c_b Dôkaz : Tbrojuholníky BCC₁ a ABC sú podobné ( uu ). Preto platí : Taktiež trojuholníky ACC₁ a ABC sú podobné ( uu ). Preto platí : Euklidova veta o výške Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka spustenou na preponu sa rovná obsahu pravouholníka, ktorého strany sú úseky na prepone priľahlé k odvesnám. v² = c_a . c_b Dôkaz : Súčet uhlov BCC₁ a CBC₁ je 90^o. Rovnako súčet uhlov BCC₁ a ACC₁ je 90^o. Odčítaním týchto vzťahov dostaneme rovnosť uhlov ACC₁ a CBC₁. Preto sú trojuholníky ACC₁ a CBC₁ podobné ( uu ). Odtiaľ dostávame :