Úlohy:
Príklad č.1Daná je kocka A-H. Zistite, či BH kolmé na ACF.
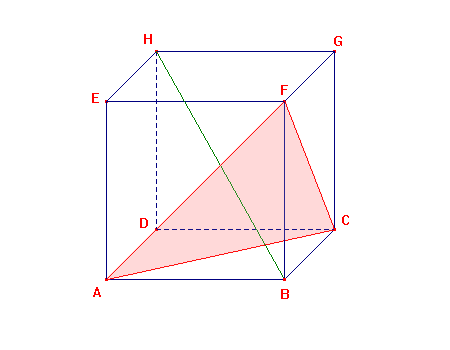
Priamka BF je kolmá na priamku AC roviny ABC. AC kolmá na BD. Vidíme teda, že priamka AC je kolmá na rôznobežné priamky BF a BD roviny BDF, preto je kolmá na rovinu BDF, a teda aj na jej priamku BH, podľa toho BH je kolmé na ACF
Príklad č.2
Body P, Q sú vnútorné body hrán FG, AB kocky A-H. Zistite, či je priamka PQ kolmá na rovinu ABC.
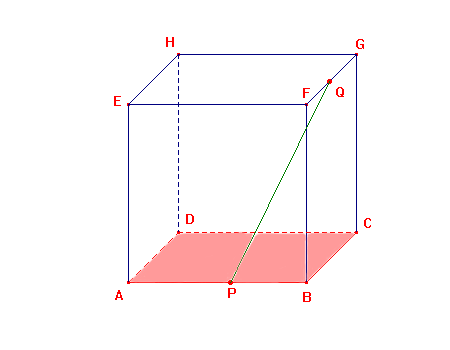
Vieme, že BF je kolmé na ABC, lebo kváder je kolmým hranolom. Ak by priamka PQ bola tiež kolmá na rovinu ABC, tak by podľa vety: Všetky priamky kolmé na tú istú rovinu sú navzájom rovnobežné, by bola rovnobežná s priamkou BF, čo nie je pravda, lebo je s ňou mimobežná. Preto priamka PQ nie je kolmá na rovinu ABC.