Množiny bodov s danou vlastnosťou
Definícia:
Množina všetkých bodov s danou vlastnosťou V v rovine je množina  bodov v rovine, ktoré spĺňajú tieto dve požiadavky:
bodov v rovine, ktoré spĺňajú tieto dve požiadavky:
- každý bod množiny
 má požadovanú vlastnosť V,
má požadovanú vlastnosť V,
- každý bod roviny, ktorý má danú vlastnosť V, patrí do množiny
 .
.
Množinami všetkých bodov s danou vlastnosťou môžu byť priamky, kružnice, rôzne iné útvary, ich časti alebo zoskupenia,
môžu to byť aj súbory izolovaných bodov a v niektorých prípadoch sa môže stať, že v hľadanej množine bodov nieje ani jeden bod.
Pripomeňme si teraz najznámejšie a najčastejšie využívané množiny bodov s danou vlastnosťou:
- Kružnica k(S;r).
- Os úsečky AB.
- Os uhla AVB.
- Osi uhlov
- Os p pásu .
- Ekvidištanty priamky p.
- Kružnicové oblúky o1, o2.
- Talesova kružnica.
- Dve kružnice k1, k2.
- Priamka p kolmá na t.
Množiny všetkých bodov s danou vlastnosťou sa v geometrických úvahách vyskytujú veľmi často.
Existujú dva druhy úloh, v ktorých využívame množiny bodov s danou vlastnosťou:
- nájdite množinu všetkých bodov s danou vlastnosťou (vyžadujú dôkaz),
- zostrojte geometrické miesto bodov danej vlastnosti (ide vlastne o využitie známych množín všetkých bodov s danou vlastnosťou v konštrukčných úlohách).
1. Úlohy typu: Nájdite množinu všetkých bodov s danou vlastnosťou
Pri riešení úloh tohto typu ide o to, aby sme vyhľadali všetky body v rovine, ktoré majú určitú vlastnosť. Niekedy hľadanú množinu zistíme na prvý pohľad, inokedy si pomáhame tak, že zostrojíme určití počet bodov
danej vlastnosti a na základe toho vyslovíme domnienku, ktorú potom musíme dokázať. Pri dokazovaní zistíme, či naša domnienka bola správna. Ak nie, musíme ju opraviť.
Dôkaz môžeme urobiť dvomi spôsobmi:
- priamo z definície množiny všetkých bodov s danou vlastnosťou,
- pomocou totožnosti dvoch bodových množín.
Postup pri dôkaze z definície
- Označíme
 množinu všetkých bodov, o ktorých predpokladáme, že sú riešením, teda že majú vlastnosť V.
množinu všetkých bodov, o ktorých predpokladáme, že sú riešením, teda že majú vlastnosť V.
- Dokážeme, že každý prvok množiny
 má vlastnosť V.
má vlastnosť V.
- Dokážeme, že každý bod roviny, ktorý má vlastnosť V, je prvkom množiny
 . Táto časť sa zvyčajne dokazuje vo forme obrátenej implikácie, teda dokazujeme, že každý bod, ktorý nepatrí množine
. Táto časť sa zvyčajne dokazuje vo forme obrátenej implikácie, teda dokazujeme, že každý bod, ktorý nepatrí množine  , nemá vlastnosť V.
, nemá vlastnosť V.
- Urobíme záver: Z definície množiny všetkých bodov s danou vlastnosťou vyplýva, že nami zvolená množina
 je riešením úlohy.
je riešením úlohy.
Postup pri dôkaze pomocou totožnosti dvoch bodových množín
- Označíme
 množinu všetkých bodov, ktoré sú riešením úlohy, čiže množinu všetkých bodov, ktoré majú vlastnosť V.
množinu všetkých bodov, ktoré sú riešením úlohy, čiže množinu všetkých bodov, ktoré majú vlastnosť V.
- Označíme
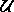 množinu všetkých bodov, o ktorých predpokladáme, že sú riešením úlohy.
množinu všetkých bodov, o ktorých predpokladáme, že sú riešením úlohy.
- Dokážeme, že množiny
 a
a 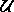 sú totožné.
sú totožné.
- Urobíme záver: Z dôkazu vyplýva, že množina
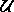 je riešením úlohy.
je riešením úlohy.
Kedy sú dve bodové množiny totožné
Dve bodové množiny 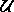 ,
,  sú totožné práve vtedy, keď každý bod X roviny spĺňa súčasne podmienky:
sú totožné práve vtedy, keď každý bod X roviny spĺňa súčasne podmienky:
- ak bod X patrí do množiny
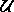 , potom patrí aj do množiny
, potom patrí aj do množiny  - inými slovami: množina
- inými slovami: množina 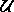 je časťou množiny
je časťou množiny  (
( 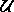 je podmnožinou
je podmnožinou  ),
),
- ak bod X patrí do množiny
 , potom patrí aj do množiny
, potom patrí aj do množiny 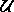 - inými slovami: množina
- inými slovami: množina  je časťou množiny
je časťou množiny 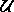 (
(  je podmnožinou
je podmnožinou 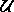 ).
).
Dôkaz totožnosti množín  a
a 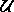
Totožnosť množín  a
a 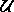 môžeme dokázať takto:
môžeme dokázať takto:
Dokážeme, že každý bod množiny  je bodom množiny
je bodom množiny 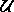 (každý bod množiny
(každý bod množiny  má vlastnosť V).
má vlastnosť V).
Potom dokážeme, že každý bod množiny 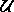 patrí množine
patrí množine  (každý bod, ktorý má požadovanú vlastnosť V, patrí množine
(každý bod, ktorý má požadovanú vlastnosť V, patrí množine  ).
).
 je podmnožinou
je podmnožinou 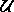 a
a 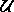 je podmnožinou
je podmnožinou  z čoho vyplýva, že
z čoho vyplýva, že  =
=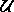 .
.
Poznámka: Ak sa nad oboma spôsobmi hlbšie zamyslíme, zistíme, že postup v oboch prípadoch je rovnaký, v oboch dokazujeme to isté. Odlišná je iba forma zápisu riešenia (v dôkaze cez definíciu používame iba jednu množinu bodov -  , v dôkaze pomocou totožnosti množín používame dve množiny bodov -
, v dôkaze pomocou totožnosti množín používame dve množiny bodov -  ,
, 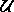
2. Konštrukčné úlohy s využitím množín všetkých bodov s danou vlastnosťou
Pri riešení konštrukčných úloh v rovine hľadáme a zostrojujeme jeden alebo niekoľko neznámych bodov. Každý z nich je charakterizovaný svojimi vlastnosťami, ktoré musíme zistiť. Tieto vlastnosti nám umožňujú zaradiť neznáme body do niektorých množín všetkých bodov s danou vlastnosťou. Ak poznáme dve takéto vlastnosti neznámeho bodu, resp. neznámych bodov,
môžeme zostrojiť dve príslušné množiny všetkých bodov s danou vlastnosťou. (Body, ktoré spĺňajú jednu z podmienok, tvoria istú množinu  1, body, ktoré spĺňajú druhú podmienku tvoria množinu
1, body, ktoré spĺňajú druhú podmienku tvoria množinu  2.)
Riešením úlohy sú spoločné body týchto množín (prienik množín
2.)
Riešením úlohy sú spoločné body týchto množín (prienik množín  1 a
1 a  2). Ak je prienikom prázdna množina, úloha nemá vyhovujúce riešenie.
2). Ak je prienikom prázdna množina, úloha nemá vyhovujúce riešenie.
 má požadovanú vlastnosť V,
má požadovanú vlastnosť V, .
.![]() má požadovanú vlastnosť V,
má požadovanú vlastnosť V,![]() .
.