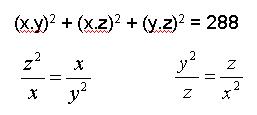Supermat

Séria č. 4 / 2000

1. V množine R riešte danú rovnicu, kde parameter t patrí R
   tx² + (t³ + t)x = 2t - 3t³


2. Daný je výraz V. Ukážte, že V⁶ = p + 1


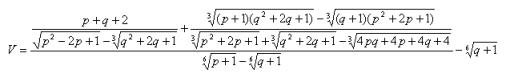
3. Počet prvočísel je nekonečný. (Euklidov dôkaz) Dôkaz sporom:
   Predpokladajme, že počet prvočísel je konečný, t.j. existuje konečná množina P={p₁, p₂, ..., p_n}, kde p₁, p₂, ..., p_n sú všetky existujúce prvočísla. Vytvorme číslo N=1+p₁p₂...p_n. Toto číslo nemôže byť deliteľné žiadnym z uvedených prvočísel, pretože vždy dostávame zvyšok 1. Na druhej strane číslo N je číslo väčšie ako 1 a teda samo je buď prvočíslo alebo je to zložené číslo, ktoré potom musí byť deliteľné prvočíslom alebo prvočíslami, ktoré nie sú uvedené v množine P. Obe tieto možnosti demonštrujú existenciu prvočísla p, ktoré nie je uvedené v pôvodnej množine. Z toho vyplýva, že naša množina nie je úplná, matematicky presne vyjadrené, množina prvočísel nie je konečná.
   Úloha:
   Pri demonštrácii tohoto dôkazu sa niektorí študenti pozastavujú, resp. považujú za zbytočné uvažovať možnosť, že číslo N je číslo zložené - pravdepodobne preto, že je vytvorené súčinom niekoľkých prvočísel zväčšeným o číslo 1.
   Nájdite aspoň päť zložených čísel tvaru N=1+p₁p2...p_n!!!



4. Riešte sústavu v R x R x R: