Supermat
Séria č. 1 / 2000
- Nájdite všetky reálne korene rovnice:
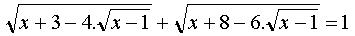
- Nájdite rovnicu, ktorej korene sú štvorcami koreňov rovnice
x3 + 3x2 + 5x + 1 = 0 .
(Návod- Možno postupovať podľa nasledujúcich vzťahov: Pre rovnicu tretieho stupňa
x3 + a1x2 + a2x + a3 = 0 platí
x1 + x2 + x3 = -a1 ; x1x2 + x1x3 + x2x3 = a2; x1x2x3 = -a3;
kde x1, x2, x3 sú korene danej rovnice. Týmto vzťahom hovoríme Vietove vzorce.)
- Dokážte, že v ľubovoľnom trojuholníku je súčet dĺžok jeho ťažníc väčší ako 3/4 obvodu trojuholníka a menší ako tento obvod.
- Číslo n4+4 nie je prvočíslo pre žiadne prirodzené číslo n >= 2. Dokážte.