|
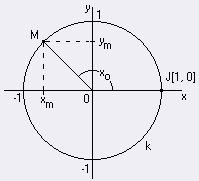
Function sinus is function, which gives to every x ╬ R ym. Funkcia cosinus is function, which gives to every x ╬ R prira´uje xm. |
| Definition field of function sinus and cosinus is set R. |
| In table are shown values of functions sinus a cosinus in several points of interval <0, 2p). |
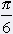 = 30░ = 30░ |
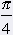 = 45░ = 45░ |
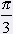 = 60░ = 60░ |
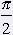 = 90░ = 90░ |
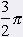 = 270░ = 270░ | |||
 |
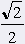 |
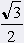 |
|||||
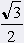 |
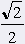 |
 |
| Both function are periodic with period 2p, which is also their smalest period. |
|
Sentence: For every k ╬ Z and for every x ╬ R is sin(x + k.2p) = sin x cos(x + k.2p) = cos x |
 |
|
We see (unitary circle) that For every x ╬ <0, 2p) is |cos x| ú 1 a |sin x| ú 1. Both function are according to that in interval <0, 2p) down and up limited. Function y = sin x: Maximum in x1 = p/2 on interval <0, 2p) Minimum in x2 = 3/2p on interval <0, 2p). sin (-x) = -sin x => uneven graf = sÝnusoid |
|
Function y = cos x Maximum in x3 = 0 on interval <0, 2p) Minimum in x4 = p on interval <0, 2p). cos (-x) = cos x => even graf = cosÝnusoid |
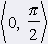 |
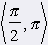 |
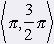 |
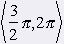 |
|
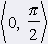 |
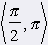 |
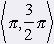 |
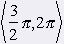 |
|
| Additional tasks |