| y = 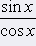 Funkcia kotangens je daná rovnicou y = 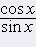
|
Definičným oborom funkcie tangens je množina všetkých tých reálnych čísel x, pre ktoré má zmysel výraz 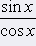 . To je práve vtedy, keď cos x ą 0. V intervale <0, 2p) sa hodnota funkcie kosínus rovná nule pre . To je práve vtedy, keď cos x ą 0. V intervale <0, 2p) sa hodnota funkcie kosínus rovná nule pre 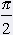 a a 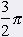 . . |
Definičným oborom funkcie y = tg x je množina všetkých reálnych čísel rôznych od 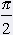 + 2kp a + 2kp a 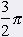 + 2kp, kde k Î Z. + 2kp, kde k Î Z. |
Inak povedané, definičným oborom funkcie y = tg x je množina všetkých x Î R, pre ktoré x ą (2k + 1)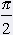 , pričom k Î Z. , pričom k Î Z.
|
Definičným oborom funkcie kotangens je množina všetkých tých reálnych čísel x, pre ktoré má zmysel výraz 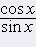 . To je vtedy, keď sin x ą 0. V intervale <0, 2p) sa hodnota funkcie sínus rovná nule pre čísla 0 a p. Z toho vyplýva, že definičným oborom funkcie y = cotg x je množina všetkých takých x Î R, pre ktoré sa x ą kp, pričom k ľubovoľné celé číslo. . To je vtedy, keď sin x ą 0. V intervale <0, 2p) sa hodnota funkcie sínus rovná nule pre čísla 0 a p. Z toho vyplýva, že definičným oborom funkcie y = cotg x je množina všetkých takých x Î R, pre ktoré sa x ą kp, pričom k ľubovoľné celé číslo.
|
|
Veta:
Nech k je ľubovoľné celé číslo. Pre každé reálne číslo x, x ą (2k + 1) 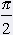 , platí: , platí:tg(-x) = -tg x, a pre každé reálne číslo x, x ą kp, platí: cotg(-x) = -cotg x. |
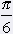 = 30° = 30° |
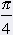 = 45° = 45° |
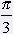 = 60° = 60° |
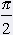 = 90° = 90° |
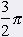 = 270° = 270° | |||
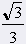 |
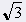 |
||||||
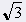 |
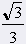 |
|
Funkcie tangens i kotangens sú teda nepárne. Vieme, že funkcie y = sin x, y = cos x sú periodické s periódou 2p. Z toho vyplýva, že aj funkcie y = tg x a y = cotg x sú periodické a jedna z ich periód je 2p. Pre každé x z definičného oboru funkcie y = tg x totiž platí: 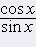 kde k Î Z. |
| K podobnému záveru môžeme dôjsť aj pre funkciu kotangens. Pri štúdií tangens a kotangens sa preto stačí obmedziť na interval <0, 2p). |
Funkcia y = tg x je množina všetkých dvojíc [x, ym], kde x ą (2k + 1)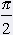 . Funkcia y = cotg x je množinou všetkých dvojíc [x, yn], kde x ą kp. . Funkcia y = cotg x je množinou všetkých dvojíc [x, yn], kde x ą kp. |
|
Veta : Nech k je ľubovoľné celé číslo. Pre každé x ą (2k + 1) 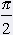 platí: platí:tg (x + kp) = tg x a pre každé x ą kp platí: cotg(x + kp) = cotg x | ||
|
Pretože najmenšia perióda funkcie tangens je p, stačí pri jej priebehu obmedziť sa na niektorú jej časť, ktorej definičný obor je otvorený interval dĺžky p. Rovnako je to v prípade funkcie kotangens.
Skúmajme napr. funkcie
k1: y = tg x, x Î (-p/2, p/2)
k2: y = cotg x, x Î (0, p) Funkcie k1 a k2 majú tieto vlastnosti: Nie sú ohraničené Ani jedna nemá maximum ani minimum Oborom funkčných hodnôt je v obidvoch prípadoch množina všetkých reálnych čísel. Funkcia k1 je rastúca na celom intervale (-p/2, p/2) Funkcia k2 je klesajúca na intervale (0, p) Nasledujúce tabuľky ukazujú, v ktorých častiach definičných oborov funkcií k1 a k2 sú ich hodnoty kladné resp. záporné čísla. |
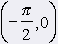 |
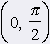 | |
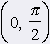 |
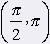 | |
| Ďalšie úlohy |