|
Funkcia sínus je funkcia, ktorá každému x Î R priraďuje ym. Funkcia kosínus je funkcia, ktorá každému x Î R priraďuje xm. |
| Definičným oborom funkcií sínus a kosínus je množina všetkých reálnych čísel. |
| V tabuľke sú uvedené hodnoty funkcií sínus a kosínus v niektorých bodoch intervalu <0, 2p). |
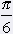 = 30° = 30° |
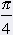 = 45° = 45° |
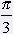 = 60° = 60° |
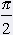 = 90° = 90° |
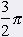 = 270° = 270° | |||
 |
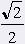 |
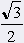 |
|||||
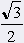 |
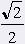 |
 |
| Z definície funkcie sínus a kosínus bezprostredne vyplýva, že obidve sú periodické a majú periódu 2p, ktorá je súčasne ich najmenšou periódou. |
|
Veta: Pre každé k Î Z a pre každé x Î R platí sin(x + k.2p) = sin x cos(x + k.2p) = cos x |
 |
|
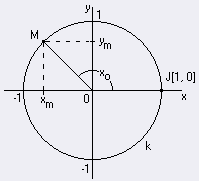
Z jednotkovej kružnice na obrázku vidíme, že pre všetky x Î <0, 2p) platí |cos x| Ł 1 a |sin x| Ł 1. Obidve funkcie sú podľa toho v intervale <0, 2p) zhora i zdola ohraničené. Funkcia y = sin x: Maximum v bode x1 = p/2 na intervale <0, 2p) Minimum v bode x2 = 3/2p na intervale<0, 2p). sin (-x) = -sin x => nepárna graf = sínusoida |
|
Funkcia y = cos x Maximum v bode x3 = 0 na intervale <0, 2p) Minimum v bode x4 = p na intervale<0, 2p). cos (-x) = cos x => párna graf = kosínusoida |
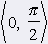 |
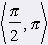 |
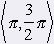 |
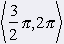 |
|
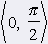 |
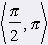 |
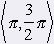 |
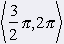 |
|
| Ďalšie úlohy |