Mocninová funkcia

Definícia :
Mocninovou funkciou sa nazýva funkcia, ktorá je daná rovnicou: y = xⁿ kde n je celé číslo.

I. Najprv zameriame svoju pozornosť na mocninové funkcie y = xⁿ, kde n Î N; pôjde o funkcie definované na množine R všetkých reálnych čísel.
Dve z týchto funkcií už poznáme: lineárnu y = x¹ a kvadartickú funkciu y = x².
Jednotlivé grafy týchto funkcií : y = x¹ , y = x² , y = x³ , y = x⁴ , y = x⁵ , y = x⁶ .

II. Uvažujme teraz o funkcii y = x⁰. Ide o funkciu definovanú na množine R - {0} alebo o funkciu
y = 1, x Î (-Ą, 0)Č(0, Ą),
ktorú už poznáme.

Niektoré vlastnosti funkcií y = xⁿ pre n Î N uvedieme v tabuľke.

1) f: y = xⁿ, n ł 0

n - nepárne		n - párne
f - nepárna		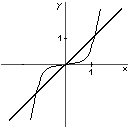f - párna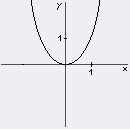
H(f) = R		H(f) = (0, Ą )
f - rastúca		minimum = f(0)
I., III. kvadrant		I., II. kvadrant

III. Nakoniec sa venujeme funkciám y = xⁿ, kde n ÎZ^-1, ktoré sú definované na množine R - {0}.

Pre n = -1 dostaneme funkciu y = x^-1, čiže ide o funkciu y = 1/x, s ktorou sa môžte oboznámiť pri funkcii nepriama úmernosť. Tu uvedieme len jednu malú, ale dôležitú poznámku:
Body grafu y = 1/x môžeme získať tak, že zostrojíme graf y = x a pre zvolené hodnoty premennej x v grafe hľadáme k hodnotám tejto funkcie ich prevrátené hodnoty. Podobne môžeme využitím grafov funkcií y = x² a y = x³ zostrojiť grafy funkcií y = x^-2 a y = x^-3.

Nasledujúca tabuľka udáva prehľad o vlastnostiach funkcií y = xⁿ pre všetky n Î Z^-.

2) f: y = xⁿ, n < 0

n - nepárne		n - párne
f - nepárna		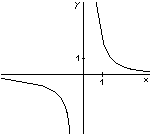f - párna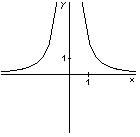
H(f) = R - {0}		H(f) = R ⁺
f - klesajúca na (-Ą, 0) rastúca na (0, Ą)		f - klesajúca na (0, Ą) rastúca na (-Ą, 0)
nie je ohraničená		ohraničená zdola

Príklady :
Príklad 1 :	Určte hodnoty funkcií y = x³, y = x⁴, y = x⁵, y = x⁶ v týchto bodoch x : -3, -2, -1, - 1/2, - 1/4, 0, 1/4, 1/2, 1, 2, 3. Využite pritom, ak to bude vhodné, známe vety o mocninách; napríklad to, že pre každé x Î R platí ( x ³ ) ² = x ⁶ atď.
Ďalšie úlohy